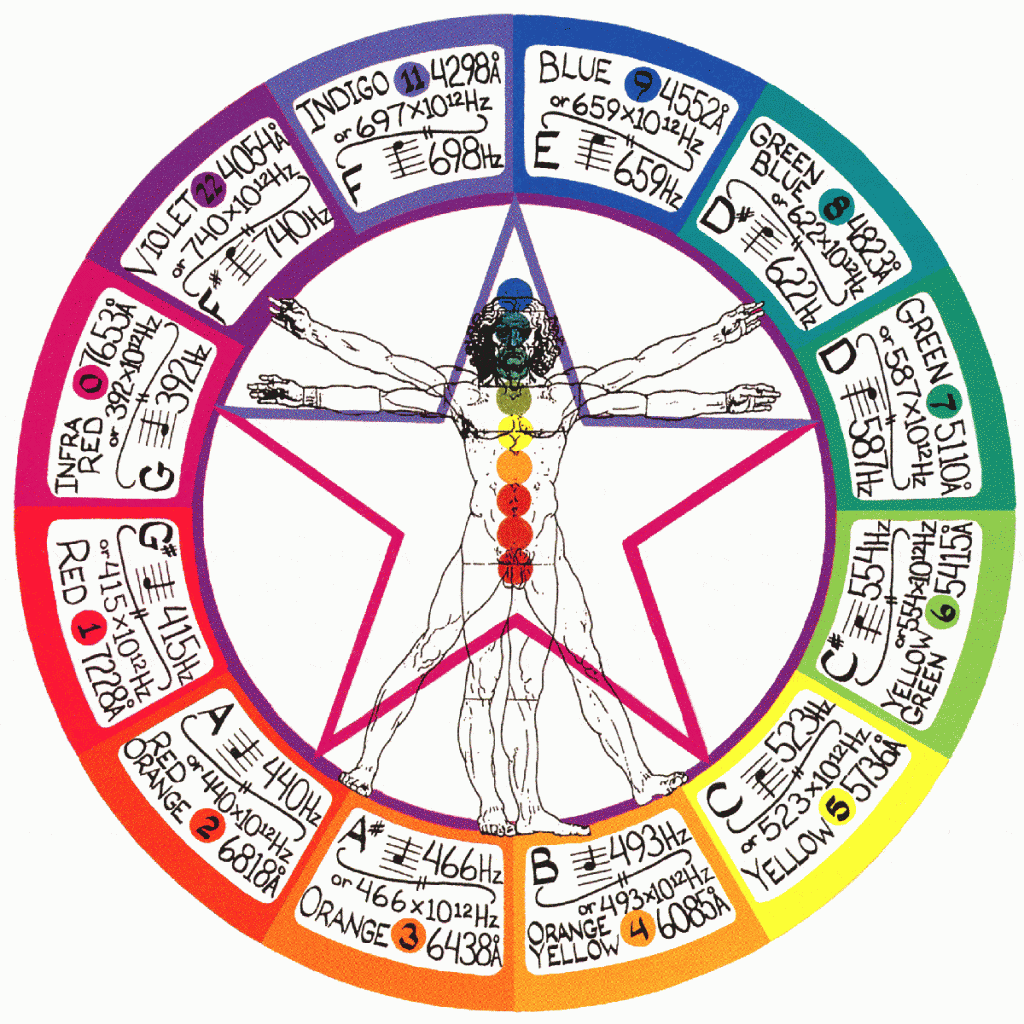
Correspondence Between Musical Notes and Visible Colors
Frequency X Wavelength = Speed of Light (299,792 km/s)
Expanded Look at Musical Octaves and Visible Color Spectrum
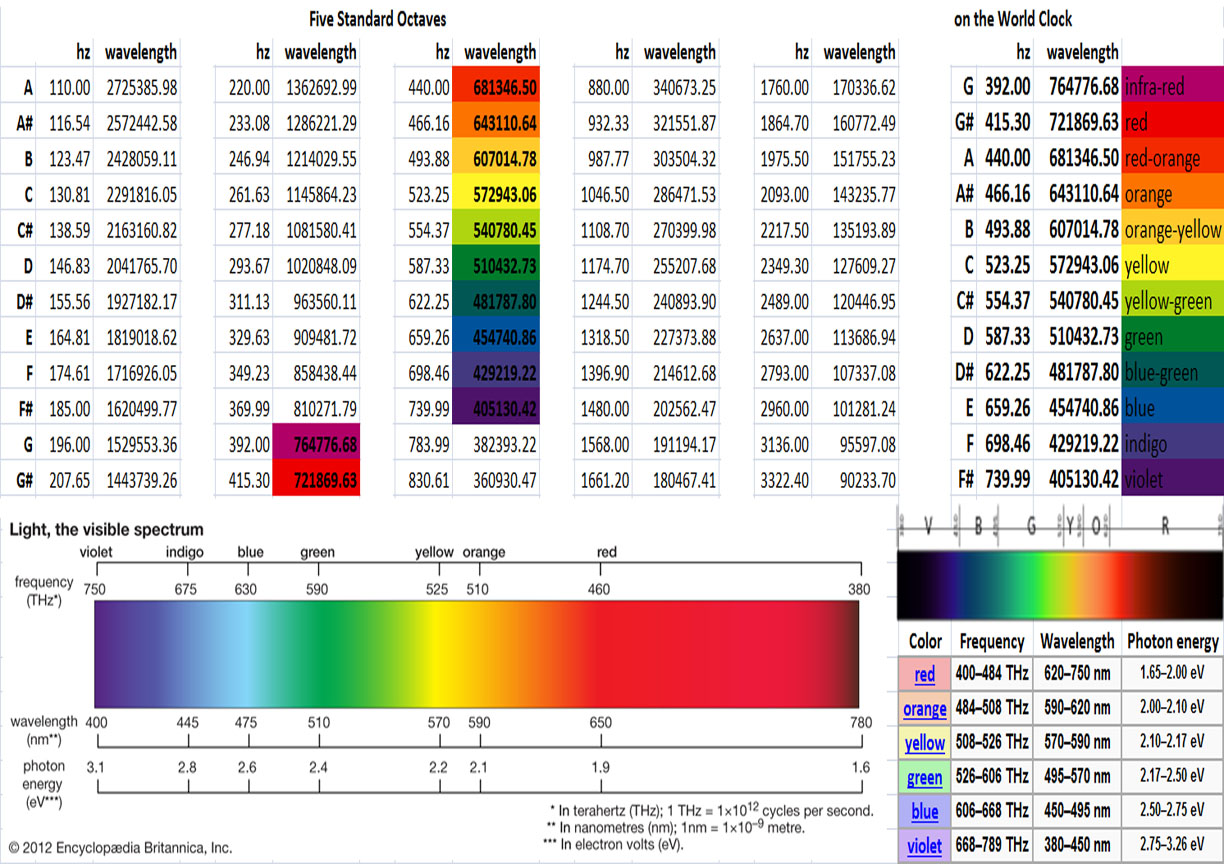
Musical Frequencies and Color Wavelengths
An Example of Resonant Harmony
It’s been years since doing my original calculations on sound and color. Way back when, prior to owning my first real computer, these columns of numbers were figured on little scraps of paper. To keep the whole process as simple as possible, I rounded the Speed of Light to 300,000,000m/s, making those big, scary numbers that much easier to tap into my hand held calculator. Due to this earlier rounding off, the numbers presented here regrettably don’t match those found upon the World Clock poster. Any resulting confusion is unintended…
There’s really no complicated formula to calculating the wavelength for any given frequency. It’s basically just: C/hz=m, although in this instance, I’ve used the more accurate C=299,792,458m/s rate for the Speed of Light. One very rudimentary formula, copied, pasted, and pulled down spread sheet columns. Math really is so much more fun when you allow a computer program to do the work!
This main table is comprised of five full octaves, with the rainbow zone located more or less at the center. Columns of musical notes with their established frequencies are presented top to bottom, listed A through G#, while the right sidebar World Clock octave is arranged from G to F#. Below my tables, visible light reference data is provided by Wikipedia, and Encyclopedia Britannica. Organized around broader color schemes than the twelve divisions found on the World Clock, these two examples were selected for their assumed credibility, and because both present frequency and wavelength together.
By applying this very simple C/hz=m formula to each musical note in turn, those cycles per second are converted into their corresponding meter wavelengths, essentially flipping each number over from one side of the scale to the other. According to data seen here, the rainbow octave actually lies above Middle C/262hz, centering in around the A/440hz pitch scale. So then, starting with G/392hz as the first note, this offset octave continues through C/523hz, and finishes up with F#/740hz.
Now with frequency and wavelength displayed side by side, pay attention to how as the frequency increases, the wavelength correspondingly decreases. Then compare the numbers for this particular musical octave, to those associated with the spectrum of visible light. Within each is found a repeating numerical progression, a hidden pattern running parallel through both phenomena. For instance, that G note at 392hz/7647m is close to the 400Thz/780nm estimation for far Red, and F# at 740hz/4051m is roughly near to 750Thz/400nm on the extreme fringe of Violet.
Better still, consider the frequency and wavelength for C at 523hz/5729m, which is virtually identical to Britannica’s 525Thz/570nm given for the color Yellow, or what about that D at 587hz/5104m, with Green at 590Thz/510nm. Finally, after all the remaining colors are compared against Wikipedia’s admittedly broader spectrum of numbers, my own placement for each particular color would appear to fall well within the specified ranges.
Once all the notes on a keyboard are calculated in this way, we find only a single musical octave matching this signature pattern. This alignment of the visible spectrum within a musical octave, based upon a harmonious convergence of frequencies and wavelengths, is why color and sound share their sympathetic resonance with one another. Consider too the sole distinction separating these vibratory tones from their corresponding colors are the 42 octaves in between, stretching out 1012 further along the scale from sound into visible light.
It’s certainly a challenge to keep all these large numbers straight, and mistakes by well intentioned amateurs like myself are not uncommon. Charts with similar content will instead focus upon the lower ‘Middle C/262hz’ octave, or perhaps have E centered on Yellow, although data here suggests E/659Thz would be more in blue to indigo color range. Suspect people are either following another esoteric tradition, or repeating errors made by others, or concocted some formula that simply works better with their own metaphysical reasoning. As for me, these are just the numbers I came up with, and can only offer these as my reasons why.
So then, of what practical use does this correspondence between music and color serve? Might this resonant coupling, signifying the inseparable unity shared by light and sound, hold any tangible scientific applications? Perhaps the true importance of these resonance patterns resides in their capacity to be reflected in different ways, to be manifest in diverse forms, and integrated into the underlying principles of various belief systems. Not unlike how frequency and wavelength are two sides of the same energetic coin, guess I’ll keep flipping reality over and over again, if only to see what turns up next!
Color which, like music, is a matter of vibrations, reaches what is most general and therefore most indefinable in nature: its inner power…
– Paul Gauguin






